К вопросу о формировании универсальных учебных действий в процессе преподавания элективного курса по математике

Тема 13. Плоские графы. Плоский граф. Грань. Соседние грани. Формула Эйлера. Графы и как примеры графов, не являющихся плоскими. Двойственные графы. Теорема Эйлера для многогранников. Правильный граф.

Тема 14. Эйлеровы графы. Эйлеров цикл. Эйлеров граф. Эйлеров путь. Критерии эйлеровости и полуэйлеровости графа.

Тема 15. Отношения и графы. Отношение. Способы задания отношений. Унарное, бинарное и тернарное отношение. Свойства и примеры отношений. Уточнение определения графа с применением понятия "отношение”.

Отметим, что раздел "Комбинаторика" не является абсолютно новым для школьников. Однако на завершающем этапе обучения нам представляется необходимым систематизировать и углубить имеющиеся знания учащихся естественно-математического профиля, которые, несомненно, будут востребованы в дальнейшем при обучении в вузах. Кроме того, комбинаторика и графы являются взаимопроникающими разделами, то есть многие комбинаторные задачи удобно решать графовыми методами, вместе с тем ряд задач теории графов предполагает наличие у учащихся основных комбинаторных знаний.

С точки зрения формирования УУД, выбранные разделы позволяют рассмотреть с учащимися основные ситуации, в которых решению задачи может предшествовать моделирование ее условия с помощью графов (полные, связные, регулярные, двудольные, ориентированные графы, деревья).

Далее остановимся на некоторых методических подходах к формированию и совершенствованию перечисленных выше видов учебных действий в процессе преподавания элективного курса "Элементы дискретной математики” учащимся классов естественно-математического профиля.

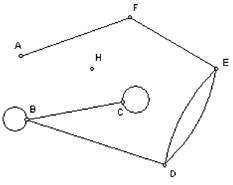
Рис. 1

Основным видом деятельности, осуществляемым на уроках математики, является решение задач. Задачи, отобранные для решения на элективном курсе "Элементы дискретной математики” могут быть, как правило, отнесены к одному из двух видов.

1. Задачи на подведение под понятие и выведение следствий.

Действие "подведение под понятие" (распознавание объектов, выделение существенных признаков и их синтез) является одним из важных логических УУД. Задания такого типа важны на этапе знакомства с новым понятием.

Среди перечисленных утверждений выберите то, которое верно для заданного графа в (рис.1): а) в мультиграф с одной изолированной вершиной и двумя вершинами степени 3; б) в псевдограф с одной висячей вершиной; в) в псевдограф, сумма степеней вершин которого равна 14; г) в мультиграф, имеющий 6 вершин и 8 ребер.

Какой из следующих графов является изоморфным графу в (рис.2)?

2. Задачи на моделирование.

Моделирование относится к знаковосимволическим УУД. Оно позволяет выделить существенное в предложенном учебном материале и преобразовать объект изучения в пространственно-графическую или знаково-символическую модель, с которой можно работать, используя общие законы данной предметной области, в данном случае дискретной математики.

3. На концерте каждую песню исполняли двое артистов, и никакая пара не выступала вместе более одного раза. Всего было 12 артистов, каждый выступал по 5 раз. Сколько было песен?

Решение. Рассмотрим граф, в котором вершины артисты; если артисты вместе пели, то вершины в графе соединены ребром. Таким образом, имеем ребер столько песен было спето.

Таким образом, здесь мы применили метод математического моделирования, знакомый школьникам из курса алгебры и состоящий из 3-х этапов: составление математической модели (перевод задачи на язык графов); работа с математической моделью (решение задачи с использованием свойств графов); ответ на вопрос задачи (перевод задачи на естественный язык и интерпретация полученного результата).

Статьи по теме:

Внедрение современных образовательных технологий
Серьёзные шаги предприняты в части обеспечения доступа в Интернет как средства расширения информационного поля обучающихся и педагогов. Информационно-коммуникационные технологии являются важным ресурсом совершенствования системы образования, позволяющим обеспечить его доступность и качество, повыси ...

Здоровье и здоровый образ жизни как целевые параметры социально-педагогической работы
Роль социального педагога в воспитании культуры здоровья трудно переоценить. Однако успешная реализация этой важнейшей социальной задачи может осуществиться при определенном уровне подготовленности педагогов, включающей широкий круг знаний, навыков и умений. Всю свою деятельность по формированию ЗО ...

Программа образования и воспитания МДОУ «Детский сад № 165»
Детский сад работает по комплексной программе «Детство». Программа «Детство» является результатом многолетней научно-исследовательской работы коллектива кафедры дошкольной педагогики Российского государственного педагогического университета им. А. И. Герцена. В ее основу легли теоретические взгляды ...